コロナ禍じゃなかったら◯◯代はもっと安かったかも！？ Causal Impact で科学的に推論した結果

「あるビールについてテレビCMを打ったら、その日から売上額が10%伸びた」

では、伸びた売上額 10% は、全てテレビCMの効果なのか？　というと、実はそうとは限りません。CMを打った期間とお花見シーズンが被っていたり、たまたま気温が高い日が続き、ビールを欲しがる人が増えただけ、という可能性もあります。

今回は、ここでいう「テレビCMの効果」を統計学的に推定する方法の一つ、「Causal Impact」（無料で使える統計分析ツール）を使って、「コロナで増えたビール代」がいくらなのか、推論してみました。

こんなグラフが最終アウトプット。ソースコードや見方の説明は後述します。

今回の例では「新型コロナウイルス感染症による緊急事態宣言/まん延防止等重点措置」をある種のキャンペーンと捉え、世帯あたりのビールへの支出額（※）にどれほどの効果・影響をもたらしたかをみてみました。
※外食は含まない。スーパーやコンビニなどで売られている缶や瓶のビール

果たして、「コロナで家飲みが増えた」は科学的に証明できるのでしょうか。
それでは行ってみましょう！

Causal Impact って何？

結論から言うと、Causal Impact は「差分の差分法」の発展版です。
差分の差分法とは、例えば、店舗Aと店舗Bで商品aについて、店舗Aでのみキャンペーンを打ったという場合、店舗Aと店舗Bのキャンペーン前後でそれぞれ売上の差分を取り、さらに店舗間の差分を差し引いて、キャンペーンの効果とするものです。

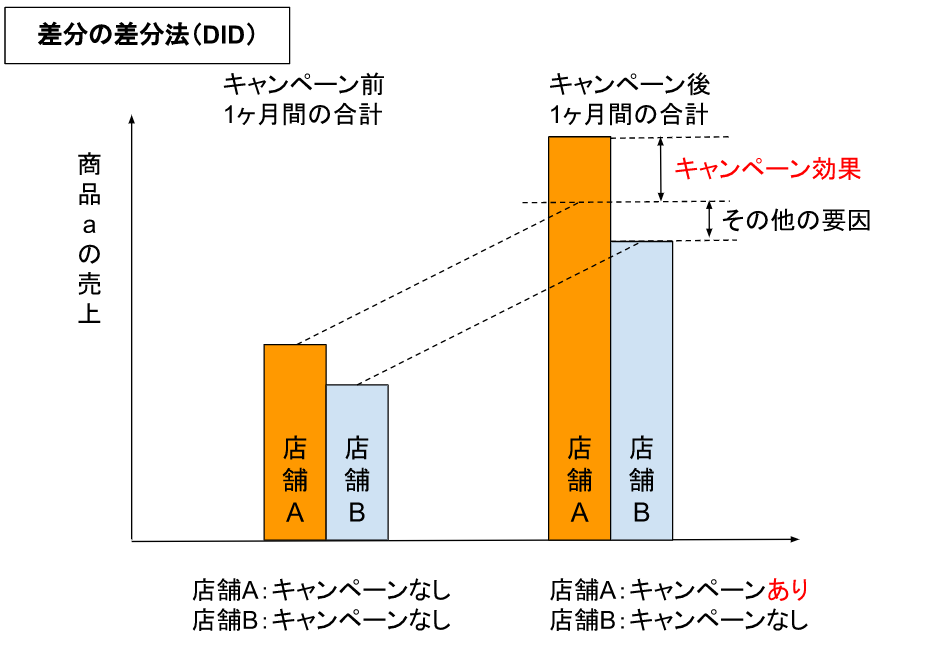
ただ、差分の差分法で正しくキャンペーン効果を算出するには、店舗Aと店舗Bで商品aの売上推移がほぼ平行であること（平行トレンド、という）、キャンペーンの他に一方の店舗のみに影響する出来事がないこと、などが前提となります。
この要件をきちんと満たす実測データ、となると、現実世界で揃えるのはなかなか難しいです。

例えば、商品aについて全店舗でキャンペーンを打った場合、店舗Aと店舗Bの差はわかりません。

そこで、Causal Impact の出番です。
Causal Impact では、非対象群の時系列データを使い、「キャンペーンを打たなかった世界線での店舗Aの商品aの売上（下図の青線）」を予測し、実測値と比較することでキャンペーン効果を算出します。

ただし、非対象群のデータは対象群の波形と似ている必要があります。これを、平行トレンド仮定、と呼んだりします。
下図では非対象群のデータを「店舗Cの商品c」としていますが、平行トレンド仮定を満たしていれば、他社の商品でも、総務省統計局の統計データでも、なんでもOKです。

これなら現実世界でも使えるやん？！　ということで、主にマーケティング界隈では有名になったツールが、Causal Impact なのです。

Causal Impact に関する Q&A

Causal Impact を使うための費用は？
→無料。オープンソースのライブラリとして、Google 社が提供してくれています。

Causal Impact は、いつ、どのタイミングで使うのか？
→キャンペーン終了後。
過去に打ったキャンペーンの効果を知りたい時に使えるのがCausal Impactです。
動かすには、観測した実データと、推論に使う非対称群の実データが必要です。

Causal Impact が使えないケースは？
→平行トレンド仮定が成り立たないケース。つまり、対象群と似た波形の非対象群のデータが取れない場合。
また、差分の差分法が使えるケースでは、Causal Impact は必要ありません。

Causal Impact の使い方 〜環境構築〜

 Mac、Windowsなど、ご自身の環境に合わせたインストーラーを、リンク先の手順で参照してダウンロード＆実行してください。
R（プログラミング言語） と RStudio（IDE） のインストール
https://posit.co/download/rstudio-desktop/

Causal Impact（Rのライブラリ）のインストール
R Studio で以下を入力します。

install.packages(“CausalImpact”) library(CausalImpact)

https://google.github.io/CausalImpact/CausalImpact.html

上記サイトにサンプルコードもあるので、興味のある人はコピペして実行してみると、Rの雰囲気もつかめていいと思います。

Causal Impact の使い方 〜データ準備〜

＜家計調査 家計収支編 二人以上の世帯　品目：ビール＞
e-Stat（総務省統計局）からデータをダウンロードします。
コロナが 2020 年以降なのでひとまず 2019 年以降を使いました。

https://www.e-stat.go.jp/dbview?sid=0003343671

対象群：東京都
非対象群：香川県　※
※波形の類似性が高い地域。選び方については別記事で解説

ここで、平行トレンド仮定をチェックします。

2019年ビールへの支出額の月次推移を比較（東京都と香川県）

相関が高く、一応グラフで確認しても乖離（東京が伸びてるのに香川は落ちてる等）があまりないことを確認します。

なお、最も相関が高かったのは実は大阪府堺市（相関係数： 0.887 ）でしたが、大阪だとコロナ対策の期間が東京とかなり被っていて Causal Impact で差を出しにくかったので二番目に相関の高い香川県としました。

＜新型コロナウイルス感染症　緊急事態宣言/まん延防止等重点措置の対象期間と地域＞
東京都と栃木県のコロナ対策期間については、以下を参照しました。

https://corona.go.jp/emergency/

弊社ではコロナ対策の地域と期間をデータ化しています。その辺の苦労話は別記事へ

それぞれ、以下の期間を確認します。

東京と香川でコロナ対策に違いが（ほぼ）ない 2019 年 1 月〜 2020 年 12月 の期間を学習用とし、
東京と香川でコロナ対策に違いがある 2021 年 1 月〜 2021 年 8 月について Causal Impact を使ってコロナの影響を推論（予測）します。

Causal Impact の使い方 〜推論の実行〜

RStudioのカレントディレクトリを RStudio > Preferences から確認し、

このディレクトリに、データを格納します。
データはこんな感じです。

データ.csv

ymd,tokyo,kagawa
2019-01-01,489,257
2019-02-01,714,71
2019-03-01,868,568
2019-04-01,828,533
…

次に、R Studio で以下を入力して実行します。

コード全体

# 1. パッケージのインストール
install.packages(“CausalImpact”)
library(CausalImpact)
library(dplyr)

# 2. データセット読み込み
data <- read.csv(“データ.csv”)

time.points <- seq(as.Date(“2019-01-01”), as.Date(“2021-08-01”), by = “months”)
head(tp)

data <- zoo(select(data, -c(1)), time.points)

dim(data)
head(data)

matplot(data, type = “l”)

# 3. 分析の実行
# 前提：共変量自体が介入の影響を受けていないpre.period <- as.Date(c(“2019-01-01”, “2020-12-01”)) # 学習用
post.period <- as.Date(c(“2021-01-01”, “2021-08-01”)) # 予測（推論）用

# 推論を実行
impact <- CausalImpact(data, pre.period, post.period)

# 4. 結果のプロット
plot(impact)

出力結果

デフォルトでは、プロットには 3 つのパネルが含まれています。 

＜最初のパネル（ original ）＞
Y軸：東京都区部における一世帯あたりのビールへの支出額（月）
実線：実際の観測データ
点線：推論データ（コロナがない世界線での支出額＝反事実予測）
ブルーの編みかけ：推論の 95% 信頼区間

95% 信頼区間とは、よほどのこと（＝介入）がない限りはこの範囲に収まるよ、を意味します。言い換えると、この範囲からはみ出ている＝介入の効果、ということになります。
上のグラフでは、2021 年 4 月からはみ出ていることからも、緊急事態宣言（＝介入）の影響でビールの支出額が増えたと言えます。
例えば、 2021 年 8 月の実測値は1384
コロナがなければ、ビールはこれほど売れなかったであろう、ということ。

＜ 2 番目のパネル（ pointwise ）＞
観測データと反事実予測の違いを示しています。

＜ 3 番目のパネル（ cumulative ）＞
2 番目のパネルで点ごとの寄与を合計した、介入の累積効果を示しています。
なお、最後に以下を実行すると、レポートを出力してくれます。

summary(impact, “report”)

出力されたレポート↓

During the post-intervention period, the response variable had an average value of approx. 1.38K. By contrast, in the absence of an intervention, we would have expected an average response of 0.99K. The 95% interval of this counterfactual prediction is [0.85K, 1.12K]. 

（中略）

The probability of obtaining this effect by chance is very small (Bayesian one-sided tail-area probability p = 0.001). This means the causal effect can be considered statistically significant.

なんかいろいろ書いてましたが、東京都で一世帯あたりがビールに使う支出額は、2021年1月以降（コロナ介入後）の実測値は月平均 1,380 円なのに対し、コロナがもしなかったら、990 円だったと予想されます、ってことが書いてある。

東京都では、大体 1.4 倍くらいビールに使うお金が増えたってことですね（！）

Causal Impactを使ってみた感想

コード自体は数行でかけてしまうので、データさえ用意できれば非常に簡単にキャンペーン効果を推論できる、優秀なツールだと思いました。

ただ、データの用意が思いのほか大変でした。特に、対象群と平行トレンド仮定が成り立つデータ（非対象群）が必要なのですが、これを選ぶのが難しかったですね。

推論の精度も非対称群のデータ次第なところがあるので、多少時間をかけてでも、慎重に選ぶが吉。

まとめ

• Causal Impact ではキャンペーンの効果を科学的に推論できる
• 平行トレンド仮定が成り立つ非対象群データを用意するところが一番難しい
• コロナで家飲みが増えた、は科学的にも真だった